A Trigonometria (trigono: triângulo e metria: medidas) é o estudo da Matemática responsável pela relação existente entre os lados e os ângulos de um triângulo. Nos triângulos retângulos (possuem um ângulo de 90º), as relações constituem os chamados ângulos notáveis, 30º, 45º e 60º, que possuem valores constantes representados pelas relações seno, cosseno e tangente. Nos triângulos que não possuem ângulo reto, as condições são adaptadas na busca pela relação entre os ângulos e os lados.
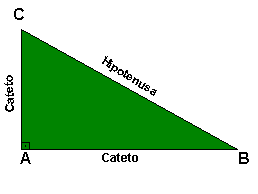
Catetos e Hipotenusa
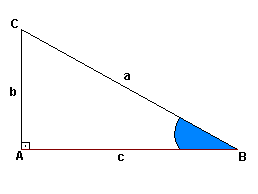
Em um triângulo
chamamos o lado oposto ao ângulo reto de hipotenusa e os lados
adjacentes de catetos.Observe a figura:
Seno, Cosseno e Tangente
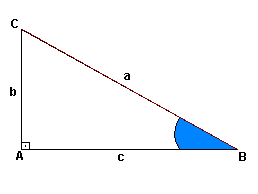
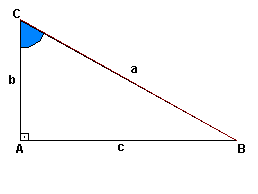
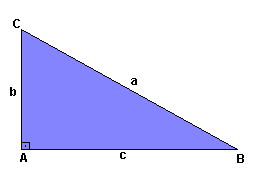
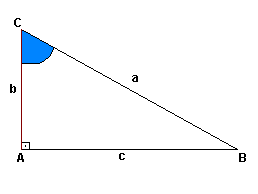
Considere um triângulo retângulo BAC:
Assim:
|
Tangente
-
Tangente de um ângulo agudo é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo.
Assim:
 |
 |
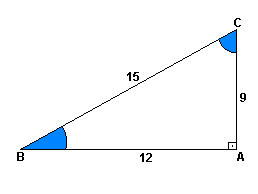
Exemplo:
 |
|
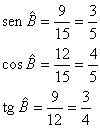 |
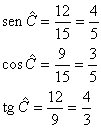 |
Observações:
1. A tangente de um ângulo agudo
pode ser definida como a razão entre seno deste ângulo e o seu cosseno.
Assim:
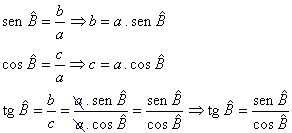
2. A tangente de um ângulo agudo é um número real positivo.
3. O seno e o cosseno de um ângulo agudo são sempre números
reais positivos menores que 1, pois qualquer cateto é sempre
menor que a hipotenusa.
As
razões trigonométricas de 30º, 45º e 60º
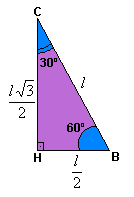
Considere as
figuras:
Seno, cosseno e tangente de 30º
Aplicando
as definições de seno, cosseno e tangente para os ângulos de 30º, temos:
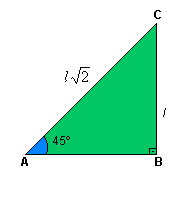
Seno, cosseno e tangente de
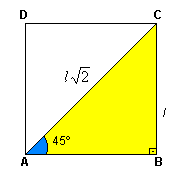
45º
Aplicando
as definições de seno, cosseno e tangente´para um ângulo de 45º, temos:
Seno, cosseno e tangente de
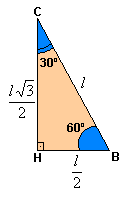
60º
Aplicando as
definições de seno, cosseno e tangente para um ângulo de 60º, temos:
Resumindo
|
| Fonte: somatematica.com.br e brasilescola.com |
Acompanhe os próximos videos do mesmo canal.

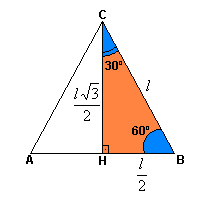
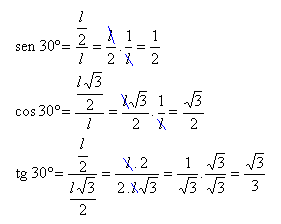
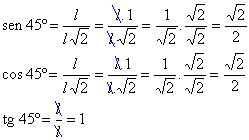
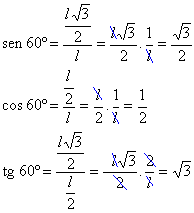


 0
Comentários
0
Comentários

