O estudo da probabilidade vem da necessidade de em certas situações, prevermos a possibilidade de ocorrência de determinados fatos.
Ao começarmos o estudo da probabilidade, normalmente a primeira ideia que nos vem à mente é a da sua utilização em jogos, mas podemos utilizá-lo em muitas outras áreas. Um bom exemplo é na área comercial, onde um site de comércio eletrônico pode dela se utilizar, para prever a possibilidade de fraude por parte de um possível comprador.
Para iniciarmos o estudo da probabilidade, vamos a seguir definir alguns conceitos importantes sobre a matéria.
Experimento Aleatório
É aquele experimento que quando repetido em iguais condições, podem fornecer resultados diferentes, ou seja, são resultados explicados ao acaso.
Exemplo:
Se lançarmos uma moeda ao chão para observarmos a face que ficou para cima, o resultado é imprevisível, pois tanto pode dar cara, quanto pode dar coroa.
Se ao invés de uma moeda, o objeto a ser lançado for um dado, o resultado será mais imprevisível ainda, pois aumentamos o número de possibilidades de resultado.
Espaço Amostral
Ao lançarmos uma moeda não sabemos qual será a face que ficará para cima, no entanto podemos afirmar com toda certeza que ou será cara, ou será coroa, pois uma moeda só possui estas duas faces. Neste exemplo, ao conjunto { cara, coroa } damos o nome de espaço amostral, pois ele é o conjunto de todos os resultados possíveis de ocorrer neste experimento.
Representamos um espaço amostral, ou espaço amostral universal como também é chamado, pela letra S. No caso da moeda representamos o seu espaço amostral por:
S = { cara, coroa }
Se novamente ao invés de uma moeda, o objeto a ser lançado for um dado, o espaço amostral será:
S = { 1, 2, 3, 4, 5, 6 }
Evento
Quando lançamos um dado ou uma moeda, chamamos a ocorrência deste fato de evento. Qualquer subconjunto de um espaço amostral é um evento.
Em relação ao espaço amostral do lançamento de um dado, veja o conjunto a seguir:
A = { 2, 3, 5 }
Note que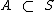 
( A está contido em S, A é um subconjunto de S ). O conjunto A é a representação do evento do lançamento de um dado, quando temos a face para cima igual a um número primo.
Classificação de Eventos:
Podemos classificar os eventos por vários tipos. Vejamos alguns deles:
Evento Simples
Classificamos assim os eventos que são formados por um único elemento do espaço amostral.
A = { 5 } é a representação de um evento simples do lançamento de um dado cuja face para cima é divisível por5. Nenhuma das outras possibilidades são divisíveis por 5.
Evento Certo
Ao lançarmos um dado é certo que a face que ficará para cima, terá um número divisor de 720. Este é um evento certo, pois 720 = 6! = 6 . 5 . 4 . 3 . 2 . 1, obviamente qualquer um dos números da face de um dado é um divisor de 720, pois 720 é o produto de todos eles.
O conjunto A = { 2, 3, 5, 6, 4, 1 } representa um evento certo pois ele possui todos os elementos do espaço amostral S = { 1, 2, 3, 4, 5, 6 }.
Evento Impossível
No lançamento conjunto de dois dados qual é a possibilidade de a soma dos números contidos nas duas faces para cima, ser igual a 15?
Este é um evento impossível, pois o valor máximo que podemos obter é igual a doze. Podemos representá-lo por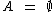 
, ou ainda por A = {}.
Evento União
Seja A = { 1, 3 } o evento de ocorrência da face superior no lançamento de um dado, ímpar e menor ou igual a 3e B = { 3, 5 }, o evento de ocorrência da face superior, ímpar e maior ou igual a 3, então C = { 1, 3, 5 }representa o evento de ocorrência da face superior ímpar, que é a união dos conjuntos A e B, ou seja, 
.
Note que o evento C contém todos os elementos de A e B.
Evento Intersecção
Seja A = { 2, 4 } o evento de ocorrência da face superior no lançamento de um dado, par e menor ou igual a 4 eB = { 4, 6 }, o evento de ocorrência da face superior, par e maior ou igual a 4, então C = { 4 } representa o evento de ocorrência da face superior par, que é a intersecção dos conjuntos A e B, ou seja,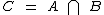 
.
Veja que o evento C contém apenas os elementos comuns a A e B.
Eventos Mutuamente exclusivos
Seja A = { 1, 2, 3, 6 } o evento de ocorrência da face superior no lançamento de um dado, um número divisor de6 e B = { 5 }, o evento de ocorrência da face superior, um divisor de 5, os eventos A e B são mutuamente exclusivos, pois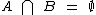 
, isto é, os eventos não possuem elementos em comum.
Evento Complementar
Seja A = { 1, 3, 5 } o evento de ocorrência da face superior no lançamento de um dado, um número ímpar, o seuevento complementar é A = { 2, 4, 6 } o evento de ocorrência da face superior no lançamento de um dado, um número par.
Os elementos de A são todos os elementos do espaço amostral S que não estão contidos em A, então temos queA = S - A e ainda que S = A + A.
Probabilidade de Ocorrência de um Evento
Os três irmãos Pedro, João e Luís foram brincar na rua. Supondo-se que as condições de retorno para casa são as mesmas para cada um deles, qual é a probabilidade de Luís voltar para casa primeiro?
Como 3 é o número total de irmãos, então Luís tem 1 chance em 3 de voltar para casa primeiro, por isto aprobabilidade de Luís voltar para casa antes dos seus irmãos é igual a 1/3.
Definição
A probabilidade de um evento ocorrer (Luís voltar para casa primeiro) considerando-se um espaço amostral(Pedro, João e Luís) é igual a razão do número de elementos do evento (1, apenas Luís) para o número de elementos do espaço amostral (3, o número de irmãos que foram brincar na rua), desde que espaço o amostral seja um conjunto equiprovável, ou seja, todos os seus elementos tenham a mesma possibilidade de ocorrer (as condições de retorno para casa são as mesmas para os três irmãos).
Sendo E um evento, n(E) o seu número de elementos, S o espaço amostral não vazio e n(S) a quantidade de elementos do mesmo, temos que a probabilidade de E ocorrer é igual a:
A probabilidade é um número entre zero e um, inclusive, o que significa que no mínimo não a nenhuma hipótese do evento acontecer e no máximo o evento sempre ocorrerá:
0 ≤ P(E) ≤ 1
Normalmente representamos probabilidades através de frações, mas também podemos representá-las por números decimais, ou até mesmo por porcentagens.
fonte: somatematica.com.br, matematicadidatica.com.br
Aula Parte 1
Aula Parte 2
Exercícios:
1 - (Fuvest) Um dado cúbico, não viciado, com faces numeradas de 1 a 6, é lançado três vezes. Em cada lançamento, anota-se o número obtido na face superior do dado, formando-se uma sequência (a, b, c). Qual é a probabilidade de que b seja sucessor de a ou que c seja sucessor de b?
a) 4/27
b) 11/54
c) 7/27
d) 10/27
e) 23/54
a) 4/27
b) 11/54
c) 7/27
d) 10/27
e) 23/54
2 - (Fuvest) Uma urna contém 5 bolas brancas e 3 bolas pretas. Três bolas são retiradas ao acaso, sucessivamente, sem reposição. Determine
a) a probabilidade de que tenham sido retiradas 2 bolas pretas e 1 bola branca.
b) a probabilidade de que tenham sido retiradas 2 bolas pretas e 1 bola branca, sabendo-se que as três bolas retiradas não são da mesma cor.
0
Comentários
